ELEMENTOS DE UNA RED NEURONAL
Los
elementos individuales de cálculo que forman los modelos de sistemas neuronales
artificiales, reciben el nombre de Elementos de Procesado o Neuronas
Artificiales. Cada unidad realiza un trabajo muy simple: recibe impulsos de
otras unidades o de estímulos externos y calcula una señal de salida que
propaga a otras unidades y, además, realiza un ajuste de sus pesos. Este tipo
de modelos, es inherentemente paralelo en el sentido de que varias unidades
pueden realizar sus cálculos al mismo tiempo. El elemento de procesado más
simple suele tener el esquema mostrado en la Fig. 1.7.
 |
Figura 1.7 Esquema de una Neurona Artificial.
|
(1.1)
Donde:
- a: es la salida de la neurona.
- Fk: es la función de transferencia de la neurona.
- Wij: es la matriz de pesos.
- Pi:es el patrón de entrenamiento.
- bk:es el umbral de activación de la neurona.
Este
esquema de elemento de procesado tiene las siguientes características:
- Cada elemento de procesado puede tener varias entradas asociadas a
propiedades diferentes.
- La entrada de tendencia es opcional (valor constante).
- Las entradas pueden ser: Excitadoras, inhibidoras, de ganancia, de
disparo fortuito o de amortiguamiento.
- Las entradas están ponderadas por un factor multiplicativo de peso
o intensidad de conexión que resaltan de forma diferente la importancia de
cada entrada.
- Cada elemento de procesado tiene un valor de activación calculado
en función del valor de entrada neto (calculado a partir de las entradas y
los pesos asociados a ellas). En algunos casos, el valor de activación,
depende además de la entrada neta del valor anterior de activación.
- Una vez calculado el valor de activación, se determina un valor de
salida aplicando una función de salida sobre la activación del elemento de
procesado.
CONEXIÓN ENTRE UNIDADES.
En la
mayor parte de los casos se asume que cada unidad recibe contribuciones
aditivas de las unidades que están conectadas a ellas. La entrada total de la
unidad k es la suma ponderada de las entradas que recibe más el término de
offset.
(1.2)
Donde:
- nk: es la salida lineal de la neurona.
- Wij: es la matriz de pesos.
- Pi:es el patrón de entrenamiento.
- bk:es el umbral de activación de la neurona.
Cuando
el peso de la contribución es positivo se considera que la entrada es
excitatoria y cuando el peso es negativo que es inhibitoria.
Este
tipo de expresiones que calculan la entrada total se denominan reglas de
propagación y, en general, pueden tener diferentes expresiones.
FUNCIONES DE ACTIVACIÓN Y SALIDA
Además
de la regla de propagación es necesario poseer expresiones para las funciones
de activación (calculan la activación en función de la entrada total) y
funciones de salida (calculan la salida en función de la activación).
La
función de activación calcula la activación de la unidad en función de la
entrada total y la activación previa, aunque en la mayor parte de los casos es
simplemente una función no decreciente de la entrada total. Los tipos de
función más empleados son: la función escalón, función lineal y la función
sigmoidal.
La
función de salida empleada usualmente es la función identidad y así la salida
de la unidad de procesado es idéntica a su nivel de activación.
Las
redes neuronales están formadas por un conjunto de neuronas artificiales
interconectadas. Las neuronas de la red se encuentran distribuidas en
diferentes capas de neuronas, de manera que las neuronas de una capa están
conectadas con las neuronas de la capa siguiente, a las que pueden enviar
información.
La
arquitectura más usada en la actualidad de una red neuronal, se presente en la
Fig. 1.8, la cual consiste en:
- Una primera capa de entradas, que recibe información del exterior.
- Una serie de capas ocultas (intermedias), encargadas de realizar el
trabajo de la red.
- Una capa de salidas, que proporciona el resultado del trabajo de la
red al exterior.
 |
| Figura 1.8 Esquema de una red neuronal antes del entrenamiento. Los círculos representan neuronas, mientras las flechas representan conexiones entre las neuronas. |
El
número de capas intermedias y el número de neuronas de cada capa dependerá del
tipo de aplicación al que se vaya a destinar la red neuronal.
FUNCIONES DE ACTIVACIÓN Y SALIDA
Un
modelo más académico que facilita el estudio de una neurona, puede visualizarse
en la Fig. 1.9.
 |
| Figura 1.9 Neurona de una sola entrada. |
Donde:
- nk: es la salida lineal de la neurona.
- Wij: es la matriz de pesos.
- Pi:es el patrón de entrenamiento.
- bk:es el umbral de activación de la neurona.
Las
entradas a la red serán ahora presentadas en el vector p, que para
el caso de una sola neurona contiene solo un elemento, w sigue
representando los pesos y la nueva entrada b es una ganancia
que refuerza la salida del sumador n, la cual es la salida neta de
la red; la salida total está determinada por la función de transferencia , la
cual puede ser una función lineal o no lineal de n, y que es
escogida dependiendo de las especificaciones del problema que la neurona tenga
que resolver; aunque las RNA se inspiren en modelos biológicos no existe
ninguna limitación para realizar modificaciones en las funciones de salida, así
que se encontrarán modelos artificiales que nada tienen que ver con las
características del sistema biológico.
Función
escalón (Hardlim)
La Fig.
1.10, muestra como esta función de transferencia acerca la salida de la red a
cero, si el argumento de la función es menor que cero y la lleva a uno si este
argumento es mayor que uno. Esta función crea neuronas que clasifican las
entradas en dos categorías diferentes, característica que le permite ser
empleada en la red tipo Perceptrón.
 |
| Figura 1.10 Función de Transferencia Escalón (Hardlim). |
(1.3)
El
ícono para la función escalón (Hardlim) reemplazará a la letra f en la
expresión general, cuando se utilice la función Hardlim.
Una
modificación de esta función puede verse en la Fig. 1.11, la que representa la
función de transferencia Escalón Simétrica (Hardlims) que restringe el espacio
de salida a valores entre 1 y –1.
 |
| Figura 1.11 Función de Transferencia de Escalón Simétrica. |
(1.4)
Función de Transferencia lineal
(purelin)
La
salida de una función de transferencia lineal es igual a su entrada, la cual se
representa en la figura 1.12.
a = n
 |
| Figura 1.12 Función de Transferencia Lineal (purelin). |
(1.5)
En la
gráfica del lado derecho de la figura 1.12, puede verse la característica de la
salida a de la red, comparada con la entrada p, más un valor de ganancia b,
neuronas que emplean esta función de transferencia son utilizadas en la red
tipo Adaline.
Función de Transferencia sigmoidal
(logsig)
Esta
función toma los valores de entrada, los cuales pueden oscilar entre más y
menos infinito, y restringe la salida a valores entre cero y uno, de acuerdo a
la expresión:
(1.6)
Esta
función es comúnmente usada en redes multicapa, como la Backpropagation, en
parte porque la función logsig es diferenciable, como se muestra en la Fig.
1.13.
 |
| Figura 1.13 Función de Transferencia Sigmoidal. |
ESTRUCTURAS GENERALES DE LAS REDES NEURONALES
PERCEPTRÓN
En
1943, Warren McCulloc y Walter Pitts originaron el primer modelo de operación
neuronal, el cual fué mejorado en sus aspectos biológicos por Donald Hebb en
1948. En 1962 Bernard Widrow propuso la regla de aprendizaje Widrow-Hoff, y
Frank Rosenblatt desarrolló una prueba de convergencia, y definió el rango de
problemas para los que su algoritmo aseguraba una solución. El propuso los
'Perceptrons' como herramienta computacional, mostrado en la Fig. 1.15.
 |
Figura 1.15 Modelo del Perceptrón Simple. |
BACKPROPAGATION
En la
red multicapa, se interconectan varias unidades de procesamiento en capas, las neuronas
de cada capa no se interconectan entre sí. Sin embargo, cada neurona de una
capa proporciona una entrada a cada una de las neuronas de la siguiente capa,
esto es, cada neurona transmitirá su señal de salida a cada neurona de la capa
siguiente. La Fig. 1.16 muestra un ejemplo esquemático de la arquitectura de
este tipo de redes neuronales.
 |
| Figura 1.16 Red Backpropagation. |
HOPFIELD
La Red
de Hopfield que se muestra en la Fig. 1.17, es recurrente y completamente
conectada. Funciona como una memoria asociativa no lineal que puedealmacenar
internamente patrones presentados de forma incompleta o con ruido. De esta
forma puede ser usada como una herramienta de optimización. El estado de cada
neurona puede ser actualizado un número indefinido de veces, independientemente
del resto de las neuronas de la red pero en paralelo.
 |
Figura 1.17 Red de Hopfield de 3 Unidades. |
KOHONEN
Existen
evidencias que demuestran que en el cerebro existen neuronas que se organizan
en muchas zonas, de forma que las informaciones captadas del entorno a través
de los órganos sensoriales se representan internamente en forma de capas
bidimensionales. Por ejemplo, en el sistema visual se han detectado mapas del
espacio visual en zonas de córtex (capa externa del cerebro). También en el
sistema auditivo se detecta organización según la frecuencia a la que cada
neurona alcanza la mayor respuesta (organización tono tópica).
Aunque
en gran medida esta organización neuronal está predeterminada genéticamente, es
probable que de ella se origine mediante el aprendizaje. Esto sugiere, por
tanto, que el cerebro podría poseer la capacidad inherente de formar mapas
topológicos de las informaciones recibidas del exterior. De hecho, esta teoría
podría explicar su poder de operar con elementos semánticos: algunas áreas del
cerebro simplemente podrían crear y ordenar neuronas especializadas o grupos
con características de alto nivel y sus combinaciones. Se trataría, en
definitiva, de construir mapas espaciales para atributos y características.


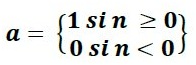


No hay comentarios:
Publicar un comentario